Homoscedasticity and heteroscedasticity

Homoscedasticity and heteroscedasticity - two of the scariest sounding terms in all of Statistics!  So what do they mean?

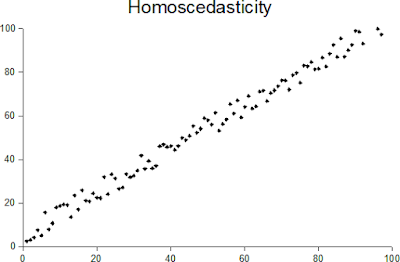
When one calculates the variance or standard deviation of a dataset of random variables, one assumes that the variance is constant across the entire population.  This assumption is homoscedasticity.  The opposite of this assumption is heteroscedasticity.



In other words, a collection of random variables is heteroscedastic if there are sub-populations within the dataset that have different variances from others (source: https://en.wikipedia.org/wiki/Heteroscedasticity).  Another way of describing homoscedasticity is constant variance and another way of describing heteroscedasticity is variable variance.



Jeremy J Taylor in his blog provides a great example of a distribution that is heteroscedastic.  In his example, the independent variable is "age" and the predictor variable is "income".  The example discusses how incomes start to vary more as age increases (as some people earn more than others as they grow older).  You can read his blog on this topic here.




Comments

Post a Comment

Popular posts from this blog

AI, ML, NN and DL: a visual explanation

Image
There appears to be a lot of confusion between the terms Artificial Intelligence (AI), Machine Learning (ML), Neural Networks (NN) and Deep Learning (DL).  Based on research from various popular blogs and articles, here is my attempt at a simple visual explanation:
Read more

Understanding And Interpreting Gain And Lift Charts

Image
Lift and Gain Charts are a useful way of visualizing how good a predictive model is. In SPSS, a typical gain chart appears as follows: In today's post, we will attempt to understand the logic behind generating a gain chart and then discuss how gain and lift charts are interpreted. To do this, we will use the example of a direct mailing company. Let us assume that based on experience, the company knows that the average response rate on its direct mail campaigns is 10%. Let us further make the following assumptions: * Cost per ad mailed = $1 * Return per response = $50 Additionally, let us assume that the company mails out ads in lots of 10,000. Based on these assumptions, if the company mails out 100,000 ads, a table summarizing the results it would obtain from this campaign is provided below: Now let us assume that the company uses SPSS Modeler to develop a predictive model using data from previous campaigns. "Response / No Response" is identified as the &
Read more