Feature selection for efficient modeling

Feature selection, also known as variable selection, feature reduction, attribute selection or variable subset selection is the technique of selecting a subset of relevant features for building robust learning models (Source: Wikipedia).  Data mining problems may involve hundreds, or even thousands, of variables that can potentially be used as inputs.  As a result, a great deal of time and effort may be spent examining which variables to include in the model.  Feature selection allows us to identify the most important variables to be used in the modeling process which can lead to the following benefits:

1. Speed up model building: by using only the most important variables in model building, feature selection enables us to significantly reduce processing times thereby speeding up model building.  The greater the number of potential "input" variables, the greater is the improvement in model building speed by using feature selection.
2. Reduction in time and cost of model building: collecting data for some variables is both time consuming and costly.  Using feature selection, resources can be focused on collecting data for only the most important variables thereby eliminating waste of time and money on less important variables.
3. Removing unimportant variables: some variables which appear to be important inputs to the model building process may turn out to have little or no predictive importance.  Feature selection helps identify these variables so they can be excluded from the model building process upfront.
4. Ease of deployment: simpler models with fewer input variables are easier to deploy and therefore more practical.  This is perhaps the most important benefit of feature selection.

In today's post, we compare two models built from the same data set: one without using feature selection and the other using feature selection.  We will use IBM SPSS Modeler v15 for our analysis.

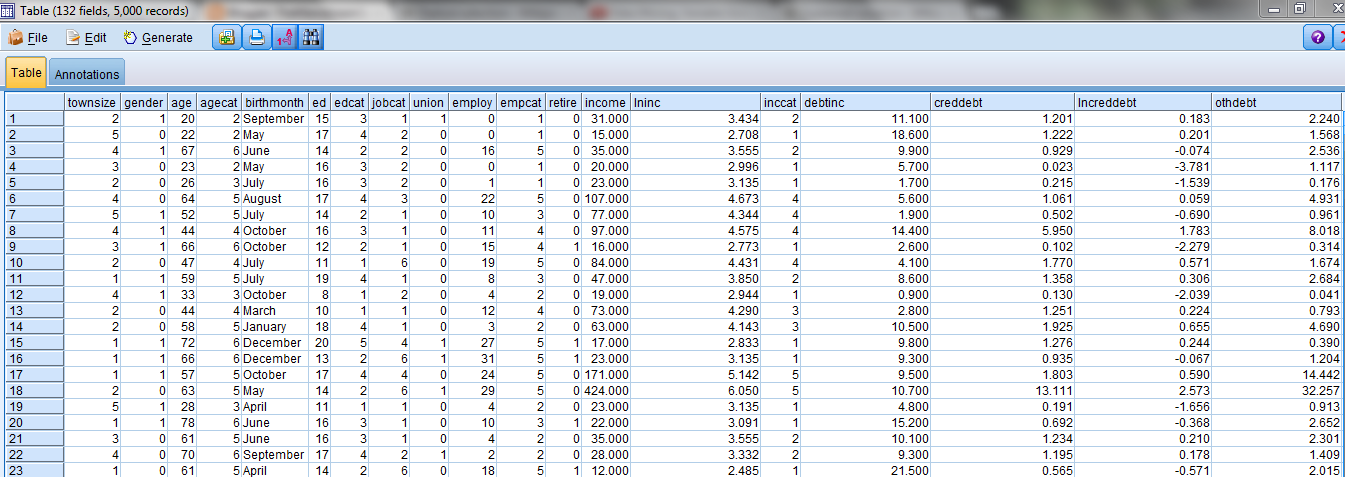
We start with a data set for a fictional telephone company that contains responses by 5,000 of its customers to three marketing offers that were previously made to them.  The company wants to use this data to predict responses to similar offers in the future.  A preview of the data set is as follows:

As can be seen this data set has 5,000 records and 132 fields.  Three of these fields contain responses to previous marketing campaigns so there are potentially 128 fields that can be used as inputs into the model building process (one of the fields is customer id which is irrelevant to the model building exercise).

Next, we attach a feature selection node to the data set and execute the node.  The results are as follows:

As can be seen from the image above, the feature selection node has classified the variables into three categories:

1. Important
2. Marginal
3. Unimportant

Furthermore, these variables are ranked in order of importance and the check boxes in the first column of the output screen enable the data scientist to choose the variables that she wishes to include in the analysis.  For the purposes of this post, we choose the top ten most important variables for our analysis and ignore the rest.

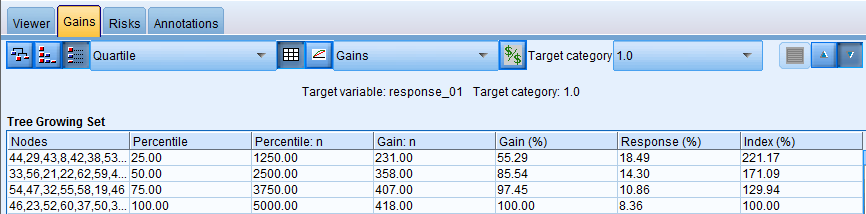
Next, we use the CHAID decision tree algorithm to build our models, both with and without feature selection.  We first look at the Gains table for the model without using feature selection:

From this table, we can see that in the first quartile of cases, the model shows a lift of 221% which means that cases that are included in the relevant nodes in the decision tree (44, 29, 43, 8, etc) are 2.2 times more likely to respond positively to a future campaign than the rest of the list.

Now we examine the Gains table for the model using feature selection:

From this table, we can see that in the first quartile of cases, the model shows a lift of 194% which means that cases that are included in the relevant nodes in the decision tree (18, 23, 15 and 12) are 1.9 times more likely to respond positively to a future campaign than the rest of the list.

On comparing our results, we see that the model that uses all variables is slightly better than our model that uses only ten variables.  However, before we draw any conclusions as to the effectiveness of using feature selection, let us turn our attention to the inputs used in each of these models.

The inputs used to obtain a 221% lift are as follows:

There are 24 inputs that need to be monitored, processed and influenced in order to obtain the lift of 221%.  In contrast, the inputs used to obtain a lift of 194% using feature selection are as follows:

As can be seen from this list, there are only 9 inputs that need to be monitored, processed and influenced in order to obtain the lift of 194%.  So for the additional lift of 0.3 (i.e. 2.2 less 1.9), an additional 15 inputs need to be considered!  In other words, in order to obtain an additional lift of approximately 16%, we need to increase the number of inputs considered by 167%!  When translated into real world scoring models, this difference can be huge in terms of time and cost savings, thereby proving the value of feature selection.